Don’t run off just yet.
Look, if you have game development aspirations, sooner or later, you’re going to have to learn linear algebra. At least a very introductory version of it.
We won’t go too deep into the math and I’ll walk through the math we encounter but we’ve already put this off long enough and we cannot continue to deeper into game development until we cover linear algebra.
Got it? Good. Then let us begin.
Why vectors?
We’ve met the vector before. We know it’s a way to bind 2 or 3 related numbers together. But vectors are also found throughout mathematics. So what and why?
A vector is just a mathematical object of one or more dimensions describing a direction and the length of that direction, what we call its magnitude.
What makes vectors really useful is its ability to simplify calculations that would otherwise be a significant challenge using other methods.
But before we get ahead of ourselves, let’s learn vectors the hard way.
Limiting ourselves to just one dimension at this time, say we have a point [a] that is 2 meters away from some other arbitrary point, 0.
We’ll call that arbitrary point the “world origin,” making point [a] 2 meters in world space and the magnitude 2 meters long.
However, magnitude only describes the length/distance of a point and lacks a direction. Is the point to the left or the right of the origin?
One more constraint is required to represent the direction.
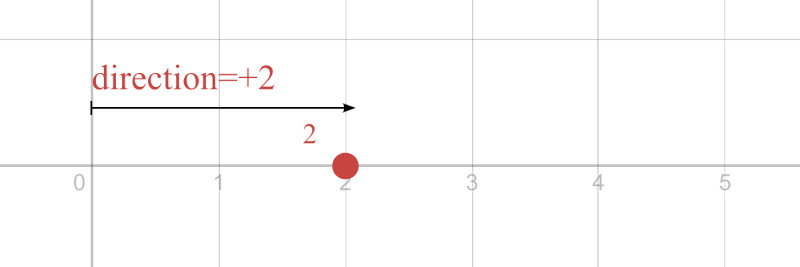
For direction, we’ll define anything to the left as the negative direction and anything to the right, positive.
So point [a] has a magnitude of 2 meters and the direction +2.
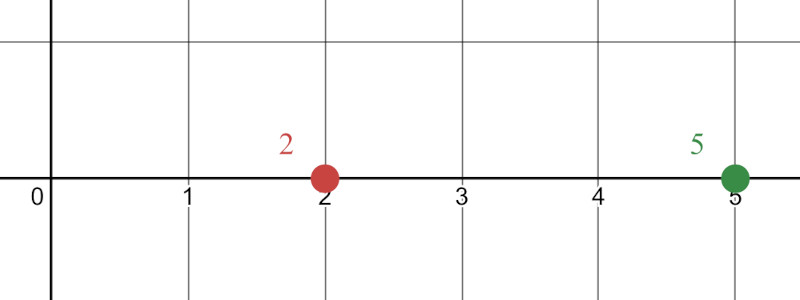
Now say there is another point [b], 5 meters from the origin and we want to find the distance and direction between [a] and [b].
Although the coordinates of the two points are relative to the origin, we can calculate a new origin by subtracting one from the other. The end result is a new localized coordinate system that describes one point relative to the other.
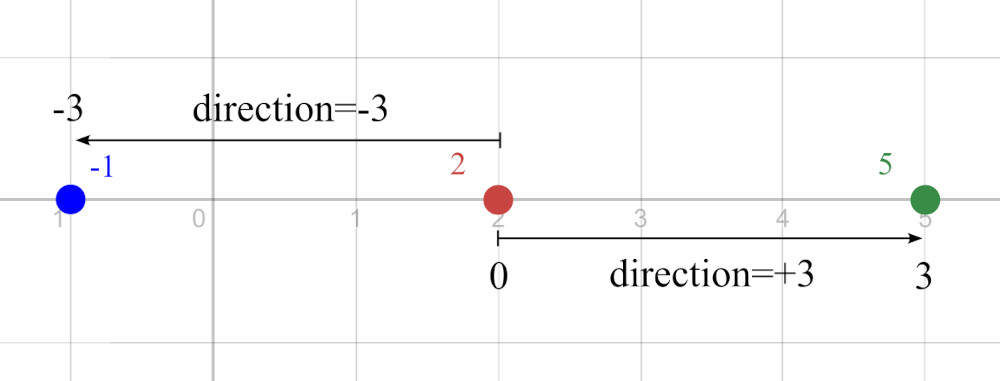
Subtracting [a] from [b] places the new origin at [a]. The resultant vector is the difference between the two original coordinates and points in the positive direction.
So for this example, the magnitude is 3 the direction is +3.
If [b] is subtracted from [a] instead, the direction is reversed. And if [b] is originally to the left of [a], that direction will be negative.
Knowing these two quantities, we can derive additional points from them.
For instance to find the point halfway between [a] and [b], take half of the distance and add it to [a]. Or for a third. Or a fourth, etc.
This idea can be extended into the next dimension. Sure, it gets a bit more challenging but giant people who came before you and I also bestowed us with more tool to work in these additional dimensions.
Vector Distance
One dimension allows us to move a point left or right. Adding a second dimension gives freedom of movement up and down.
Like before, the new dimension is also described by a number and direction.
Since these two dimensions are intrinsically linked, we need a new convention to pair them: (x, y). Where x represents the horizontal component and y the vertical.
So for the point [a] at (4, 3), it has a length of 4 in the horizontal and 3 in the vertical. The total length from the origin to the point is now a function of both dimensions.
That distance can be calculated using a formula you’ve likely already heard of before: Pythagorean’s theorem.
Start by squaring both dimensions and then take the square root of their sums. For the vector (4, 3), magnitude is 4.
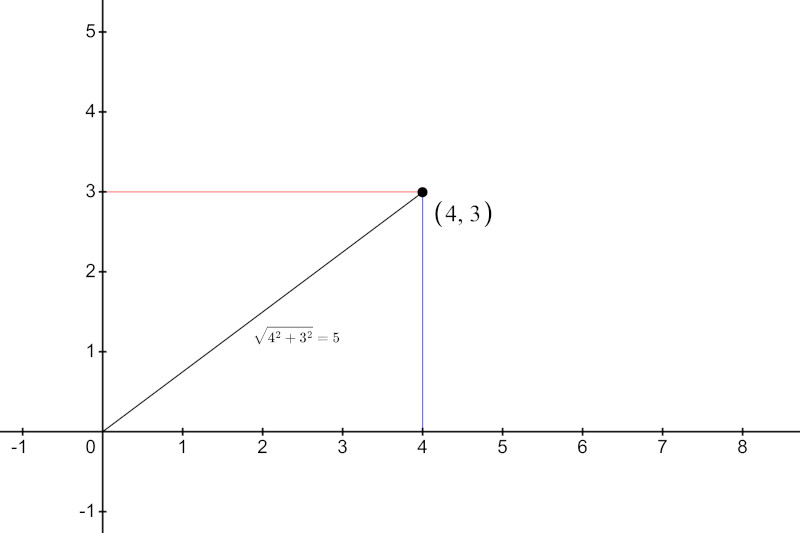
This is such a common operation that it is built in to the vector data types (Vector2 and Vector3).
local x = 4
local y = 3
local v1 = Vector2.new(x, y)
print(v1.Magnitude)
-- 5local x = 4
local y = -3
local v1 = Vector2.new(x, y)
print(v1.Magnitude)
-- 5Direction
Magnitude is a “scalar quantity” that can only be zero or a positive value, meaning magnitude lacks directional data.
And while the vector does encode the direction, in this raw form is limits usefulness because the direction is dependent on the magnitude. It needs to be decoupled from the vector to make it more generally useful.
One way to do so is to represent the direction is via an angle about some point.
The Cartesian coordinate system is already familiar so lets stick to that. We can then represent direction as an angle around the origin, where 0° aligns the vector along the x-axis.
Rotating the vector toward the positive y will sweep the vector in a counter-clockwise direction.
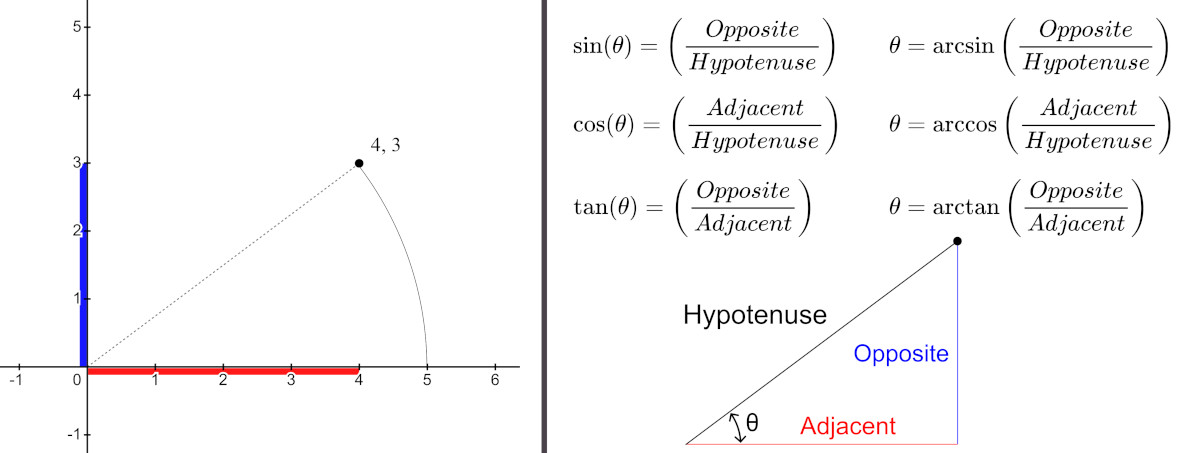
The image illustrates how the two dimensions form a triangle.
And if you didn’t skip class during geometry, then you will remember that we can use trigonometric functions to find the the sides or enclosed angles of a triangle.
Recall that the opposite side of a triangle over its adjacent side is equal to the tangent of the angle between them.
Since we know the side lengths, taking the inverse tangent gives us the angle of the vector with respect to the x-axis.
local x = 4
local y = 3
local angleRadians = math.atan(y/x)
local angleDegrees = math.deg(angleRadians)
print("Radians:", angleRadians)
print("Degress:", angleDegrees)
-- Radians: 0.6435011087932844
-- Degress: 36.86989764584402The ‘arctan’ function from the math library will return the angle in radians. This function properly handles divide by zero (x=0) cases.
But the limitation with the atan function is that it can only return angles from -π/2 to π/2 (-90° to 90°) so for a calculation that exceeds that, the result will be reversed.
local x = -4
local y = 3
local angleRadians = math.atan(y/x)
local angleDegrees = math.deg(angleRadians)
print("Radians:", angleRadians)
print("Degress:", angleDegrees)
-- Radians: -0.6435011087932844
-- Degress: -36.86989764584402The atan2 function is a variant for working with angles beyond 90°, making that the one you likely want.
local x = 4
local y = 3
local q1 = math.atan2(y, x)
local q2 = math.atan2(y, -x)
local q3 = math.atan2(-y, -x)
local q4 = math.atan2(-y, x)
print("Q1:", math.deg(q1))
print("Q2:", math.deg(q2))
print("Q3:", math.deg(q3))
print("Q4:", math.deg(q4))
-- Q1: 36.86989764584402
-- Q2: 143.13010235415598
-- Q3: -143.13010235415598
-- Q4: -36.86989764584402