The Scripting Block

3 Dimensions

In the 2D space, everything is constrained to the xy-axis. In this domain, every possible position exists on a flat plane that is perpendicular to the direction we are looking—which is in toward the screen.

This axis extending into and out of the screen is the z-axis and the final axis in our spatial realm of existence.

For the X dimension we decided on the positive direction being to the right. This is consistent with how we read/write, making it intuitive.

Similarly, in the Y dimension, increasing values are associated with up.

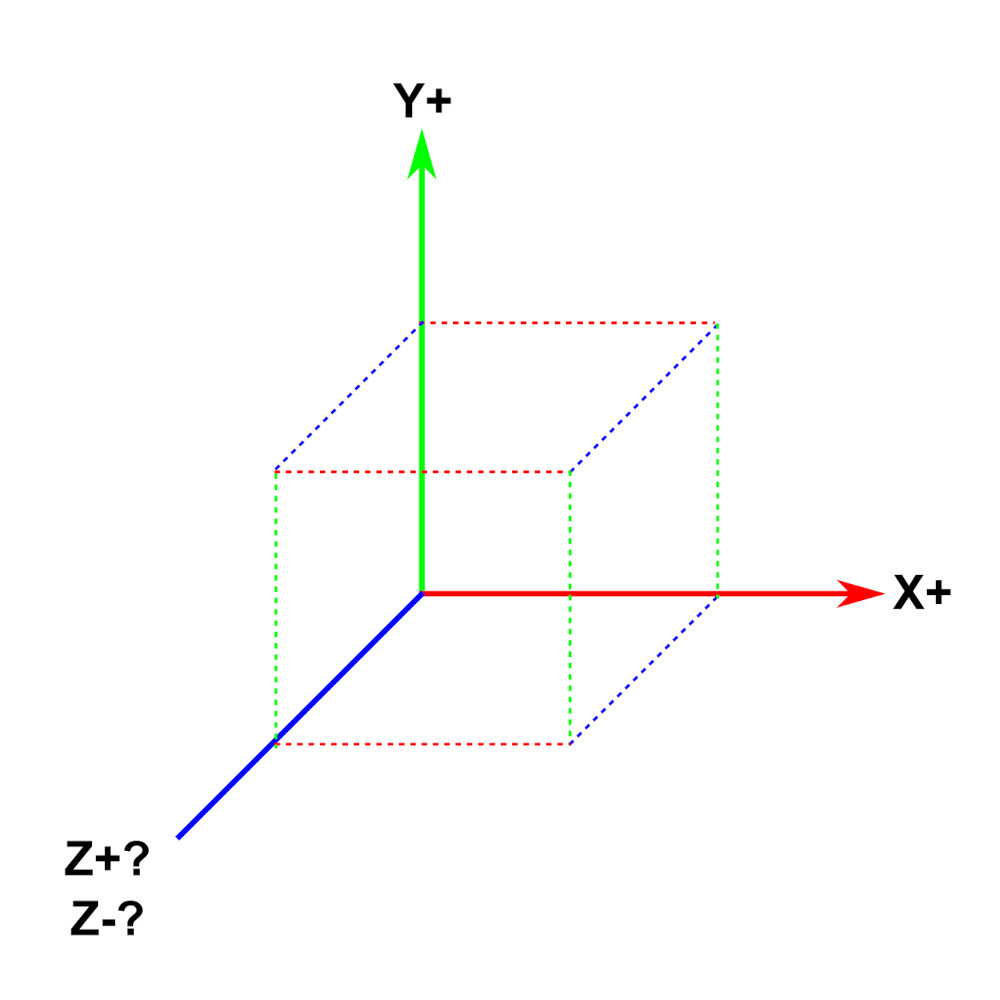
But what about the z-dimension. How do we decide which direction is positive and which is negative?

Do increasing values of Z extend forward, away from us? Or should that direction point towards us?

The Right Hand Rule

Take your right hand with palm flat, facing up and your fingers pointed horizontally in the same direction as the positive x-axis.

Then rotate you fingers into a partially closed fist so they align with the positive y-axis.

Since most of us cannot form a fist by rotating our fingers down, the arc traced by your fingers will be in the counter-clockwise direction.

And throughout the arc, your thumb will remain pointed toward you. This direction we will define as the positive z direction.

Because the right hand is required to do this, it is called the ‘right hand rule.’

However, this is not limited to just the z-axis. In 3D, this relationship is true for every axis.

When sweeping counter-clockwise from X->Y, Y->Z, and Z->X again, the positive Z, X, and Y axis always points out of the screen toward you.

In 2D, because positions are constrained to the xy plane, the angle between two vectors is always around the z-axis that is perpendicular to them.

In 3D space however, vectors are no longer constrained to the xy plane. Meaning the axis with which two vectors rotate about is also no longer constrained to the z-axis.

But angles and rotations in 3D space are still relevant, so how do we go about defining the axis to which angles are quantified?

Taking a cue from the right hand rule, when a 3D vector is rotated from an initial position to a new position, it does so around an imaginary axis that is perpendicular to both the initial and the final vector.

This vector can be calculated using the ‘cross product.’

(Run this script in a play session)

local function createPart(size, brickColor)
	local part = Instance.new("Part")
	part.Size = size
	part.BrickColor = brickColor
	part.Anchored = true
	part.Material = Enum.Material.SmoothPlastic
	part.Parent = game.Workspace
	
	return part
end

local xPart = createPart(Vector3.new(0.5, 0.04, 0.04), BrickColor.new("Really red"))
local yPart = createPart(Vector3.new(0.04, 0.5, 0.04),BrickColor.new("Lime green"))
local zPart = createPart(Vector3.new(0.04, 0.04, 0.5),BrickColor.new("Really blue"))
local plane = createPart(Vector3.new(0.01, 0.75, 0.75), BrickColor.new("Institutional white"))

plane.Shape = Enum.PartType.Cylinder
plane.Transparency = 0.5

local roll = math.random()
local pitch = math.random()
local yaw = math.random()

--uncomment to lock rotation axis
--roll = 0
--pitch = 0
--yaw = 0

local rotationCframe = CFrame.new(0, 5, 0)
local crossAngle = 0

while task.wait() do
	crossAngle = crossAngle + 1
	rotationCframe = rotationCframe * CFrame.Angles(math.rad(pitch), math.rad(yaw), math.rad(roll))
	plane.CFrame = rotationCframe * CFrame.Angles(0, math.rad(90), 0)
	
	local xCf = rotationCframe * CFrame.Angles(0, 0, math.rad(crossAngle)) --+ rotationCframe.RightVector * xPart.Size.X / 2)
	local yCf = rotationCframe
	
	xPart.CFrame = xCf + xCf.RightVector * xPart.Size.X / 2
	yPart.CFrame = yCf + yCf.UpVector * yPart.Size.Y  / 2
	local cross = xPart.CFrame.RightVector:Cross(yPart.CFrame.UpVector)
	local mag = cross.Magnitude / 2
	
	zPart.CFrame = rotationCframe + cross.Unit * zPart.Size.Z / 2
	zPart.Size = Vector3.new(0.04, 0.04, mag)
end

The script visualizes the cross product.

Given the two input vectors, green and red, the cross product of the two vectors is the blue line. The white disc is the plane that is perpendicular to the cross product.

Using the right hand rule, when you trace in the counter-clockwise direction across the shorter angle, your thumb will point in the direction of the cross product.

From the demo, we can also see that the length of the rotation vector is greatest when the input vectors are 90°.