The Scripting Block

The trig functions for useful when we want to know the angle of a vector relative to the horizontal axis. But the problem is that this only works in 2D and the angle is taken relative to the horizontal axis.

So what happens in 3D where there are two horizontal axes? Or what if we wanted the angle between two vectors

The dot product is an operation between two vectors that describes the direction of one vector relative to the other. This can be used to calculate the angle between two vectors.

Given vectors (a) and (b), the dot product describes how closely (b) aligns with (a).

If the result is positive, then both vectors are pointed in the same direction. This does not necessarily mean they are parallel. It just means their directions are within 90° of each other.

When the result is negative, (b) points in an opposite direction of (a). If the result is 0, both vectors are perpendicular to each other.

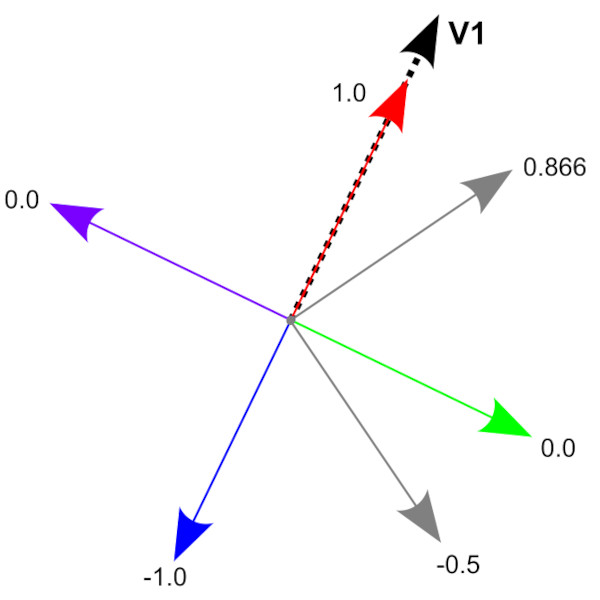
The figure above illustrates the dot product of V1 with various other vectors when they all have a length of 1.

The vector datatypes have a ‘Dot’ method that we can use to compute it.

local v1 = Vector2.new(1, 0)

local vAligned = Vector2.new(1, 0)
local vOpposite = Vector2.new(-1, 0)
local vUp = Vector2.new(0, 1)
local vDown = Vector2.new(0, -1)
local v2 = Vector2.new(0.866, 0.5)

local dotA = v1:Dot(vAligned)
local dotO = v1:Dot(vOpposite)
local dotU = v1:Dot(vUp)
local dotD = v1:Dot(vDown)
local dot2 = v1:Dot(v2)
local dot2i = v1:Dot(-v2)

print(dotA) -- 1
print(dotO) -- -1
print(dotU) -- 0
print(dotD) -- 0
print(dot2) -- 0.866
print(dot2i) -- -0.866

For the vector v1 which is aligned with the x-axis, vAligned is parallel and vOpposite is anti-parallel. Their dot products are 1 and -1 respectively.

vUp and vDown are aligned with the y-axis, making these perpendicular to v1 and their dot products 0.

The unit vector for (4, 3) points toward the same direction but not aligned, making it 0.866. The reverse of that vector points in the opposite direction and therefore negative.

This output from -1 to 1 only holds true when the vectors are magnitude 1. If one or both vectors have a length different than 1, it is reflected in the final output.

local v1 = Vector2.new(3.14, 0)

local vAligned = Vector2.new(42, 0)
local vOpposite = Vector2.new(-0.1, 0)
local vRight = Vector2.new(0, 999999)
local vLeft = Vector2.new(0, -71)

local dotA = v1:Dot(vAligned)
local dotO = v1:Dot(vOpposite)
local dotR = v1:Dot(vRight)
local dotL = v1:Dot(vLeft)

print(dotA) -- 131.880
print(dotO) -- -0.314
print(dotR) -- 0
print(dotL) -- 0

From the dot product, the angle can be calculated using the arccosine trig function.

local v1 = Vector2.new(4, 3)
local v2 = Vector2.new(3, 4)

local mag1 = v1.Magnitude
local mag2 = v2.Magnitude

local acos =  math.acos(v1:Dot(v2)/(mag1 * mag2))
local deg = math.deg(acos)
print(deg)
-- 16.260204708311967

Because these were not normalized, the dot product needs to be divided by the product of the magnitudes.

If the vectors are normalized, they can be input directly into the arccosine function.

local v1 = Vector2.new(4, 3).Unit
local v2 = Vector2.new(3, 4).Unit

local acos =  math.acos(v1:Dot(v2))
local deg = math.deg(acos)
print(deg)
-- 16.260204708311967

The Vector2 and Vector3 datatypes also have a built-angle method to directly compute the angle between two vectors.

local v1 = Vector2.new(4, 3)
local v2 = Vector2.new(3, 4)

local rad = v1:Angle(v2)
local deg = math.deg(rad)
print(rad)
print(deg)

-- 0.283794105052948
-- 16.260204708311967

Say you wanted to script a monster that patrols the map looking for players. Since the monster needs to visually see a player, how would you go about determining if a player was spotted?

It would probably involved a check to see if a player is in the monster’s cone of vision. This cone of vision is some finite angle bisected by a centerline that represents the direction of the look vector.

There needs to be two vectors, which we do have. The first vector is the monster’s look vector—this might be where the monster’s head or eyes are facing. The second vector is the vector from the monster to the player, normalized.

Taking the dot product of the two vectors yields the angle.

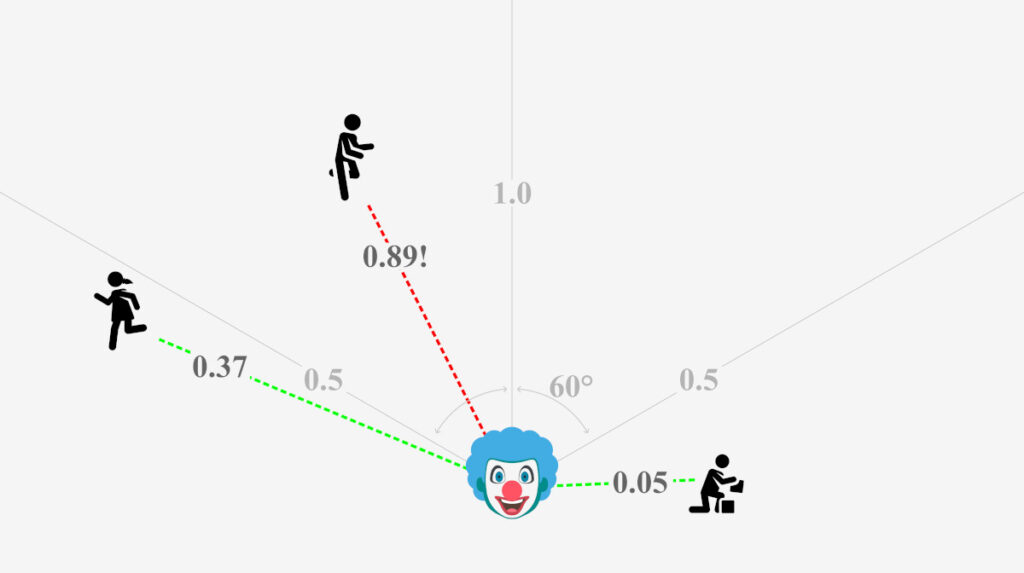
So if the monster has a 120° field of view, 60° to either side of the look vector, then any dot product greater than 0.5 represents an angle less than 60° and a player that is in the monster’s FoV.