The Scripting Block

Another way to represent direction is via some sort of “standardized” vector.

Since a vector already encodes information about the direction, this makes it easy to move a point in terms of that vector.

I mentioned earlier that in its raw form, the direction of the vector is dependent on its magnitude. Let’s temporarily call this the ‘directional’ vector.

Meaning for a 1D point at position 1, the directional vector is +1.

So moving the point by 1 directional unit moves it to 2. Moving it another unit length moves it to 3. Then 4. Then 5. Etc.

But if the point had the initial position 2, the directional vector would be +2. Moving it in that direction by 1 directional unit moves it to 4. Then 6. Then 8.

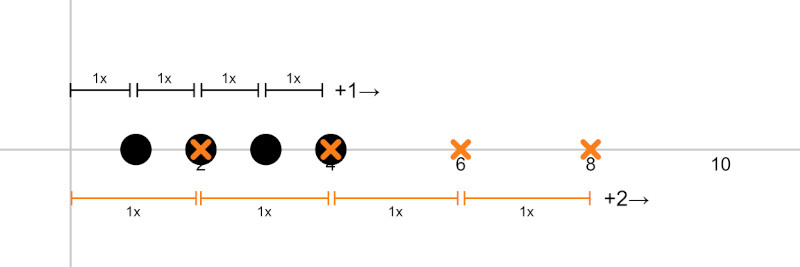
This presents a problem because even though both directional vectors point in the same direction, their lengths are not the same and therefore the distance per unit move is not the same.

Additionally, only when the directional vector has a length of 1 does it correspond nicely to our own measurement system (studs, meters, feet, etc.). This is desirable because it makes conversions between the “directional” unit and the measurement system easy.

For instance, given directional vector +1, if we wanted to move a point +12.345 meters, we can just multiply it by 12.345. Since 12.345 unit lengths of the directional vector of length 1 corresponds to 12.345 meters.

On the other hand, if the directional vector is +2, we would have to multiply it by 6.1725 to move the point 12.345 meters.

This is the idea behind the ‘unit vector’ (also known as the ‘direction vector’).

If a vector is normalized to a length of 1, then just the direction is extracted. And the result is a unitless vector that proportionately scales in each dimension when multiplied with a scalar.

The unit vector can be calculated by dividing each axis by the magnitude of the vector.

In the 1D example, this isn’t apparent because the magnitude of the vector is the same as the length of its one dimension.

Moving up to 2D, we can see this. For the point (4, 3) which has a magnitude of 5, the unit vector is:

local v2 = Vector2.new(4, 3)
local unit = v2.Unit
print(unit)
-- 0.800000012, 0.600000024

Now to move n studs in the desired direction, we just multiply it by the desired distance. So for the starting position (0, 0), the final positions are:

print(Vector2.new(4, 3).Unit * 5) --equivalent to position vector
print(Vector2.new(4, 3).Unit * 10)
print(Vector2.new(4, 3).Unit * 25)
print(Vector2.new(4, 3).Unit * 100) 
print(Vector2.new(4, 3).Unit * -100) --move in opposite direction
-- 4, 3
-- 8, 6
-- 20, 15.000001
-- 80, 60.0000038
-- -80, -60.0000038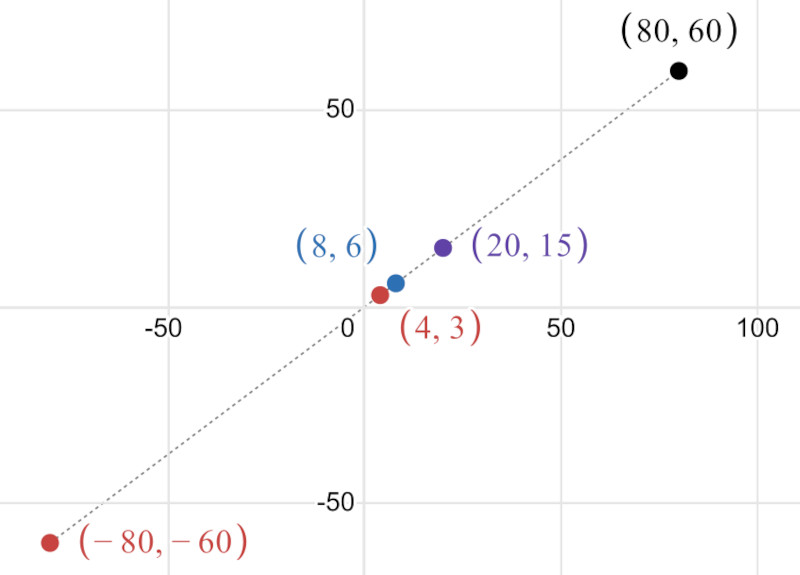

Since the unit vector is still dependent on the difference in position between two points, it is undefined when the vector length is 0.

print(Vector2.new().Unit)
print(Vector3.new().Unit)
-- NAN, NAN
-- nan, nan, nan